تابع حالت چیست؟ از اهمیت آن در انرژی درونی چه می دانید ؟

در ترمودینامیک، تابع حالت یا تابع نقطه ای (State Function, Function of State, or Point Function) به تابعی ریاضی گفته می شود که تنها به نقاط ابتدایی و انتهایی مسیر وابسته است. به عبارت دیگر، مسیر فرآیند تغییری در مقدار نهایی کمیت های حالت ایجاد نمی کند. تابع حالت، متغیر های حالت یا کمیت های حالت (که حالت‌ های تعادلی یک سیستم مثل گاز، مایع، جامد، کریستال یا امولسیون را توصیف می ‌کند)، را به یکدیگر مرتبط می ‌کند. این توابع فقط به حالت ترمودینامیکی تعادل فعلی بستگی دارند، نه به مسیری که سیستم برای رسیدن به وضعیت فعلی خود طی کرده است. به توابع حالت، توابع مستقل از مسیر نیز می گویند. در ادامه این مقاله در نشریه جهان شیمی فیزیک به بررسی توابع حالت پرداخته می شود. لطفا با ما همراه باشید.

 

تاریخچه

این احتمال وجود دارد که اصطلاح تابع حالت در طول دهه های ۱۸۵۰ و ۱۸۶۰ میلادی توسط افرادی همچون رودولف کلازیوس (Rudolf Clausius)، ویلیام رانکین (William Rankine)، پیتر تایت (Peter Tait) و ویلیام تامسون (William Thomson) به معنای آزاد بکار رفته باشد. در دهه ۱۸۷۰ میلادی، این اصطلاح کاربرد خاص خود را پیدا کرد. ویلارد گیبس (Willard Gibbs) در مقاله خود در سال ۱۸۷۳ میلادی با عنوان روش های گرافیکی در ترمودینامیک سیالات می گوید: کمیت های v، p، t، ε و η زمانی تعیین می شوند که وضعیت جسم داده شود و ممکن است مجاز باشد که آنها را تابع حالت جسم بنامیم.

 

توابع حالت و مسير

يك فرآيند شیمیایی و يا يك تغيير حالت می تواند از مسير های مختلفی صورت بگیرد. توابع ترمودینامیکی به طور کلی به دو دسته توابع مسیر و حالت تقسیم می شوند. توابع حالت به توابعی گفته می شود كه به يك حالت سیستم نسبت داده شوند. در حقیقت، براي هر حالت سیستم، يك مقدار بخصوص جهت تابع حالت وجود دارد. این توابع در هنگام تغيير حالت ممكنست تغییر كنند، اما دقت داشته باشید که مقدار تغييرات آنها تنها به حالت اوليه و حالت نهایی سیستم بستگي دارد. به بیان دیگر، مستقل از مسيري هستند كه سيستم مورد نظر به کمک آن از حالت اوليه به حالت ثانويه رفته است. به عبارت دیگر، این توابع خاصیتی از سیستم هستند که فقط به حالت فعلی آن، بستگی دارند.

لازم به ذکر است که در مقابل توابع حالت، توابع مسير وجود دارند كه به مسير طی شده به وسیله سیستم نسبت داده می شوند. این توابع می توانند مقادير متفاوتی را برای مسير های مختلفی که بين دو حالت اوليه و ثانويه يكسان وجود دارند، داشته باشند. لازم به ذکر است که استفاده از واژه تغيير (delta) برای توابع حالت معنی دارد، اما برای توابع مسير فاقد معنی خواهد بود.

 

فهرست تابع حالت

توابع حالت همان توابع يا متغير های ترموديناميكی محسوب می شوند. آنها می توانند حالت های تعادل یک سیستم را توصیف کنند، بنابراین نوع سیستم را نیز توصیف می کنند. انرژی (E)، انرژی درونی (U)، آنتالپی (H) و آنتروپی (S) نمونه ‌هایی از کمیت ‌های حالت یا توابع حالت هستند. زیرا آنها به طور کمی وضعیت تعادل یک سیستم ترمودینامیکی را بدون در نظر گرفتن اینکه سیستم چگونه به آن حالت رسیده است، توصیف می‌ کنند. برای توابع حالت همچنین می توان به دما (T)، فشار (P)، حجم (V)، انرژی آزاد گیبس (G)، انرژی آزاد هلمهولتز (F)، چگالی (P)، تعداد مول (n) و … اشاره کرد. همانطور که مشاهده می کنید، توابع حالت را با حروف بزرگ انگلیسی نشان می دهند.

در مقابل، کار مکانیکی (w) و گرما (q) کمیت های فرآیند یا توابع مسیر محسوب می شوند. زیرا مقادیر آنها به یک انتقال یا مسیر خاص بین دو حالت تعادلی اولیه و ثانویه بستگی دارد. جالب است بدانید که گرما می تواند یک تابع حالت همچون آنتالپی را توصیف کند، اما به طور کلی، سیستم را واقعا توصیف نمی کند. مگر اینکه به عنوان تابع حالت یک سیستم خاص تعریف شود. در اینصورت، آنتالپی با مقداری گرما توصیف خواهد شد.

درباره توابع مسير، علامت مثبت به معنی ورود انرژی به سيستم مورد نظر و علامت منفی به معنی خروج انرژی از سيستم مورد نظر است. اگر فرآيند گرماده باشد، علامت q منفی و اگر فرآيند گرماگير باشد، علامت q بزرگتر از صفر خواهد بود. به طور مشابه، اگر سيستم بر روی محيط كار انجام دهد و به محيط انرژی دهد، علامت كار منفی خواهد بود. در حالیکه، اگر محيط بر روی سيستم، كار انجام دهد و بنابراین سیستم از محيط انرژی بگيرد، علامت كار مثبت می شود.

 

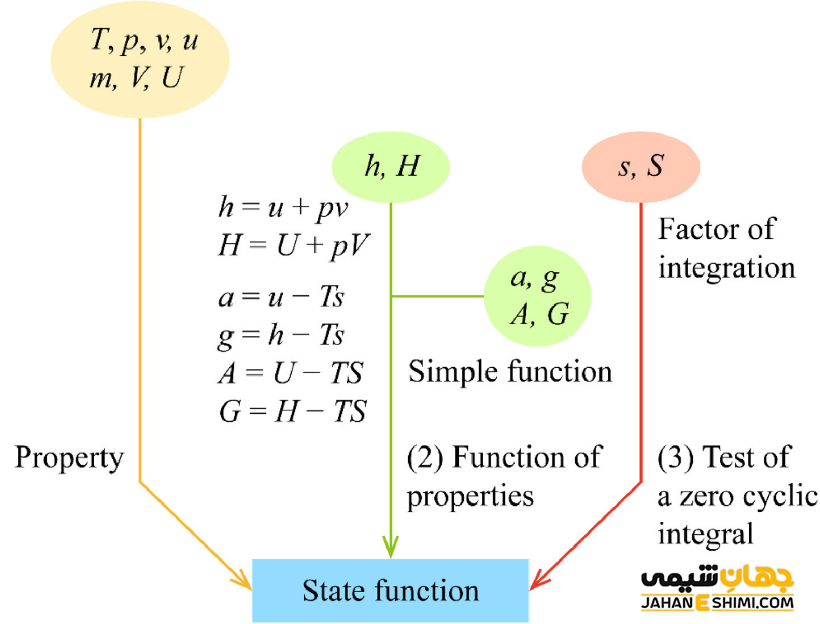
تابع حالت انرژی درونی

سیستمی را در نظر بگیرید که انرژی درونی آن در حالت اولیه x برابر با E_x و انرژی درونی در حالت نهایی y برابر با E_y است. فرض کنید، برای رفتن از حالت اولیه x به حالت نهایی y دو مسیر مختلف وجود دارد. حرکت در مسیر شماره یک، بدون مبادله گرما و تنها با مبادله کار انجام می شود. در حالیکه، حرکت در مسیر شماره دو، همزمان با مبادله گرما و مبادله کار امکان پذیر است. به طور یقین، مقدار گرما و کار در این دو مسیر با یکدیگر متفاوت است. به همین دلیل می توان گفت که گرما و کار تابع مسیر می باشند، پس به مسیر طی شده بستگی دارند.

 

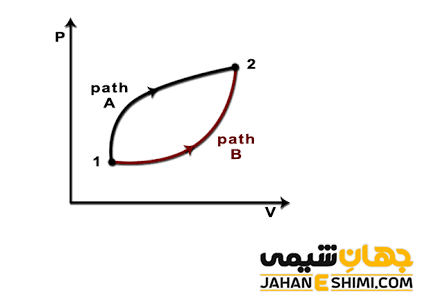
از طرف دیگر، تغییرات انرژی درونی (U∆) سیستم تابع حالت است. زیرا صرف نظر از اینکه سیستم مسیر شماره یک را طی کرده است یا مسیر شماره دو، مقدار U∆ یکسان است. در حقیقت، U∆ تابع حالت اولیه و نهایی سیستم است (U∆ = U_y – U_x) و به هیچکدام از دو مسیر بستگی ندارد. به عبارت دیگر و در بیان دیگری از قانون اول ترمودینامیک می توان گفت که تغییرات انرژی درونی (U∆) یک سامانه، مستقل از مسیر فرآیند طی شده از حالت اولیه به حالت ثانویه است و فقط به دو حالت‌ اولیه و نهایی بستگی دارد. به طور کلی می توان گفت که ممكنست انرژی درونی یك سیستم به طرق مختلف تغییر کند، اما در نهایت، انرژی درونی اهمیت دارد نه راهی كه انرژی درونی از آن طریق تغییر کرده است.

 

دیفرانسیل کامل

رابطه زیر را در تابع حالت انرژی درونی در نظر بگیرید. لازم به ذکر است که i و f به ترتیب بیانگر حالات اولیه و نهایی می باشند.

 

برای اینکه U∆ تنها به دو حالت اولیه و نهایی وابسته باشد، پس مقدار انتگرال فوق باید از مسیر فرآیند مستقل باشد. در اینصورت می توان U را به شکل یک جز بسیار کوچک (dU) تعریف کرد. بدین شکل، انتگرال از مسیر فرآیند مستقل بوده و فقط به دو حالت اولیه و نهایی بستگی دارد. به dU دیفرانسیل کامل می گویند. در اینجا می توان از انتگرال مسیر (به یک مسیر دورانی اشاره می کند که در آن، حالت اولیه و حالت نهایی برابر می باشند) بهره برد. بدین شکل انتگرال مسیر برای یک تابع حالت برابر با صفر خواهد بود.

 

تابع حالت انرژی جنبشی

به عنوان مثال، انرژی جنبشی را برای یک مولکول تنها به جرم m در سیستم در نظر بگیرید. فرض کنید، این مولکول دارای سرعت اولیه v_۱ باشد. اگر سرعت را به شکل گام به گام تا سرعت v_۴ افزایش دهید (v_۱ → v_۲ → v_۳ → v_۴)، تغییرات انرژی جنبشی به صورت زیر خواهد بود:

 

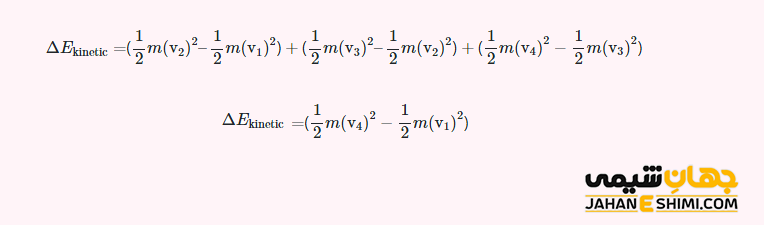
توجه داشته باشید که سرعت های v_۲ و v_۳ هر مقداری را می ‌توانند داشته باشند، اما مقادیر سرعت آنها بر نتیجه نهایی تاثیری ندارد. پس می توان گفت که تغییرات انرژی جنبشی (ΔE_kinetic)، تنها به سرعت‌ اولیه و سرعت نهایی بستگی دارد. در نتیجه مستقل از مسیر انجام شده بین این دو سرعت خواهد بود. جالب است بدانید که اگر تعداد گام‌ های سرعت نیز افزایش پیدا کند، تاثیری در نتیجه گیری نهایی ندارد. چنین تعریفی را می ‌توان به سایر شکل‌ های انرژی نیز تعمیم داد. از آنجاییکه این نتیجه گیری، برای همه مولکول‌ های موجود در سیستم صدق خواهد کرد، پس برای تغییرات انرژی درونی هم صدق می کند یعنی انرژی درونی در هر كجای سیستم ثابت خواهد بود. انرژی درونی در واقع مجموع كل انرژی ها (مجموع انرژی های جنبشی و پتانسل) است.

 

خواص ریاضی توابع حالت

یک سیستم ترمودینامیکی با تعدادی از پارامتر های ترمودینامیکی مانند دما، حجم یا فشار توصیف می‌ شود که لزوما مستقل نیستند. قانون گاز ایده آل مثال خوبی از توابع حالت است. در این قانون، یک متغیر حالت (مثلا فشار، حجم، دما یا مقدار ماده در یک سیستم تعادل گازی) تابعی از متغیر های حالت دیگر است. بنابراین به عنوان تابع حالت در نظر گرفته می شود. یک تابع حالت همچنین می‌تواند تعداد نوع خاصی از اتم‌ ها یا مولکول ‌ها را به شکل گاز، مایع یا جامد در یک مخلوط همگن یا ناهمگن، یا مقدار انرژی مورد نیاز برای ایجاد چنین سیستمی یا تغییر سیستم به سیستمی متفاوت را نیز توصیف کند.