معادله نرنست چیست؟ درباره آن چه می دانید؟

در علم الکتروشیمی، معادله نرنست (Nernst equation) به یک رابطه ترمودینامیکی شیمیایی گفته می شود که امکان محاسبه پتانسیل کاهش یک واکنش (واکنش نیمه سلولی یا تمام سلولی) را می دهد. این پتانسیل کاهش از پتانسیل استاندارد الکترود، دمای مطلق، تعداد الکترون ‌های درگیر در واکنش ردوکس و فعالیت گونه های شیمیایی تحت احیا و اکسیداسیون محاسبه می شود. لازم به ذکر است که معادله نرنست به منظور تعیین پتانسیل سلول در شرایطی به غیر از شرایط استاندارد مورد استفاده قرار می گیرد. جالب است بدانید که واکنش و نام این معادله برگرفته از والتر نرنست (Walther Hermann Nernst)، شیمیدان و فیزیکدان آلمانی بود که معادله را فرموله کرد. در ادامه این مقاله در نشریه جهان شیمی فیزیک به بررسی معادله نرنست پرداخته می شود. لطفا با ما همراه باشید.

 

معادله نرنست

همانطور که می دانید، پتانسیل سلولی استاندارد در یک شرایط استاندارد، محاسبه می گردد. در این شرایط، دما و فشار در حالت استاندارد قرار دارند و همچنین غلظت محلول آبی، ۱ مولار است. از طرفی دیگر، جهت محاسبه پتانسیل های سلولی در شرایط غیر استاندارد، معادله نرنست بکار می رود. این معادله، در حقیت به منظور محاسبه ولتاژ سلول الکتروشیمیایی مورد نظر و یا جهت پیدا کردن غلظت یکی از اجزای سلول الکتروشیمیایی، کاربرد دارد. همانطور که بیان شد، معادله نرست هم برای واکنش نیمه سلولی و هم واکنش تمام سلولی استفاده می شود. بنابراین دو رابطه مجزا داریم که عبارتند از:

پتانسیل کاهش نیم سلول

E_red = E^۰_red – (RT / zF) ln (a_Red / a_Ox)

 

در این معادله، E_Red بیانگر پتانسیل کاهشی نیم پیل، E^۰_Red بیانگر پتانسیل الکترود استاندارد، R بیانگر ثابت جهانی گاز ها (۸.۳۱۴۴۶۲۶۱۸۱۵۳۲۴ J K^−۱ mol^−۱)، T بیانگر دمای مطلق بر حسب کلوین، z بیانگر تعداد الکترون ‌هایی می باشد که در جریان الکترولیز واکنش می‌ دهند، F بیانگر ثابت فارادی (۹۶۴۸۵.۳۳۲۱۲۳۳۱۰۰۱۸۴ C mol^−۱)، و a بیانگر فعالیت شیمیایی برای گونه مورد نظر است، که در آن a_Red فعالیت گونه کاهش یافته و a_Ox فعالیت گونه اکسید شده است. با تبدیل ln به Log ، معادله به شکل زیر تغییر می کند.

E_red = E^۰_red – (۲.۳۰۳RT / zF) Log_۱۰ ^(a_Red ^{/ a}_Ox⁾

توجه داشته باشید که در شرایط اتاق، دما برابر با ۲۵ درجه سانتی گراد یا ۲۹۸ کلوین است. بنابراین با جایگزینی در معادله بالا، عبارت RTF^−۱ را برابر با ۲۵.۶۹۳ mV در نظر گرفته و معادله به شکل زیر ساده می شود.

E_red = E^۰_red – (۵۹.۱ mV / z) Log_۱۰ ^(a_Red ^{/ a}_Ox⁾

 

پتانسیل کاهش تمام سلول

E_cell = E^۰_cell – (RT / nF) lnQ

در این معادله، E_cell بیانگر پتانسیل سلول (نیروی محرکه الکتریکی)، E^۰_cell بیانگر پتانسیل استاندارد سلول، R بیانگر ثابت جهانی گاز ها (۸.۳۱۴۴۶۲۶۱۸۱۵۳۲۴ J K^−۱ mol^−۱)، T بیانگر دمای مطلق بر حسب کلوین، n بیانگر تعداد الکترون ‌های انتقالی در واکنش سلولی، F بیانگر ثابت فارادی (۹۶۴۸۵.۳۳۲۱۲۳۳۱۰۰۱۸۴ C mol^−۱) و Q بیانگر خارج قسمت واکنش است. دقت داشته باشید که معادله بالا را می توان با استفاده از خواص لگاریتم و تبدیل ln به Log به شکل زیر نوآرایی کرد.

E_cell = E^۰_cell – (۲.۳۰۳RT / nF) Log _۱۰^Q

لازم به ذکر است که در شرایط استاندارد، دما برابر با ۲۹۸ کلوین است. بنابراین عدد ۲۹۸ را می توان در معادله بالا جایگزین کرد. در اینصورت، عبارت RTF^−۱ را برابر با ۲۵.۶۹۳ mV در نظر گرفته و معادله به شکل زیر ساده می شود.

E_cell = E^۰_cell – (۰.۰۵۹۲V / n) Log _۱۰^Q

معادله فوق نشان می ‌دهد که پتانسیل الکتریکی یک سلول الکتروشیمیایی، تابعی از خارج قسمت واکنش می باشد.

 

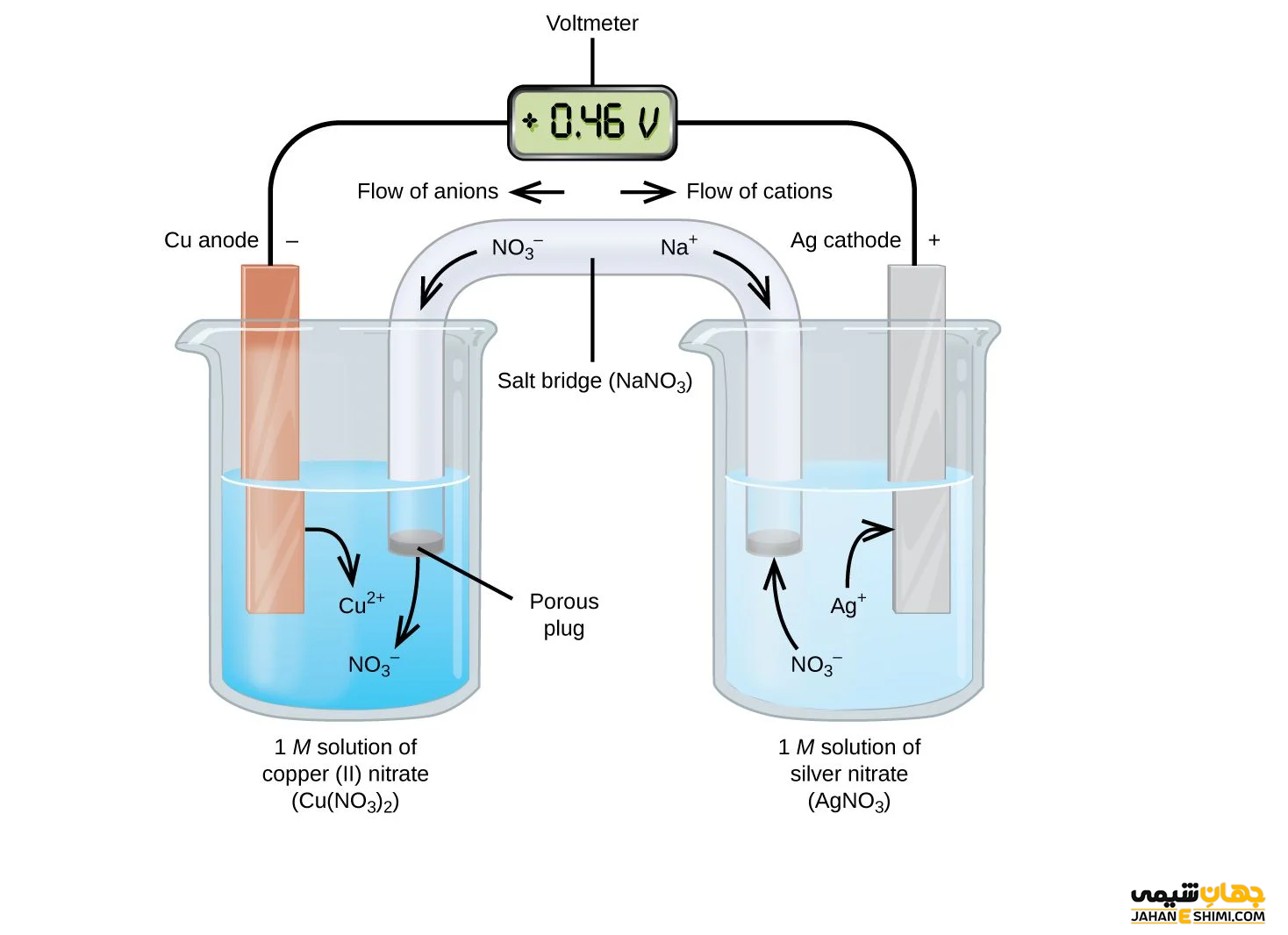
اثبات معادله

رابطه نرنست در واقع رابطه ای میان پتانسیل کاهشی یک سلول الکتروشیمیایی، پتانسیل استاندارد سلول، دما و همچنین ضریب واکنش می باشد. هنگامی که یک اکسید کننده (Ox) تعداد z االکترون را می پذیرد تا به شکل احیا شده آن (Red) تبدیل شود، نیمه واکنش به صورت زیر بیان می شود:

Ox + ze⁻ → Red

رابطه نرنست در حقیقت از انرژی آزاد گیبس در شرایط استاندارد ایجاد می شود. در اینصورت برابر با اختلاف پتانسیل استاندارد حالت کاهش و اکسایش می باشد.

E^۰ = E^۰_Red − E^۰_Ox

از طرفی دیگر، پتانسیل سلول مرتبط با واکنش الکتروشیمیایی به عنوان کاهش انرژی آزاد گیبس به ازای هر کولن بار منتقل شده تعریف می شود. از این رو، رابطه میان انرژی آزاد گیبس و اختلاف پتانسیل منجر به رابطه زیر می شود.

ΔG = −nFE

در شرایط استاندار، رابطه فوق به شکل زیر خواهد شد.

ΔG^۰ = −nFE^۰

ترمودینامیک استاندارد همچنین می گوید که انرژی آزاد واقعی گیبس (ΔG) مربوط به تغییر انرژی آزاد در حالت استاندارد (ΔG^۰) است. بنابراین می‌ توان آن را به وسیله رابطه زیر حساب کرد:

ΔG = ΔG^۰ + RT lnQ

با جایگذاری معادلات مربوط به ΔG و ΔG^۰ خواهیم داشت:

nFE = −nFE^۰ + RT lnQ−

با تقسیم طرفین رابطه بر nF−، می توان رابطه را به صورت زیر تغییر داد:

E = E^۰ – (RT / nF) lnQ

بدین شکل رابطه نرست بدست می آید.

 

معادله نرنست و غلظت

همانند ثابت‌ های تعادل واکنش های شیمیایی، فعالیت ‌ها همیشه با توجه به حالت استاندارد اندازه‌ گیری می ‌شوند. فعالیت شیمیایی یک گونه i، یعنی a_i، از طریق رابطه a_i = γ_i C_i به غلظت اندازه گیری شده (C_i) مربوط می شود. در این رابطه، γ_i ضریب فعالیت گونه i است. از آنجاییکه ضرایب فعالیت در غلظت ‌های پایین تمایل به وحدت دارند و یا در غلظت ‌های متوسط و بالا ناشناخته یا دشوار بدست می آیند، پس فعالیت ‌ها در معادله نرنست اغلب با غلظت ‌های ساده جایگزین می‌ شوند. در اینصورت، پتانسیل‌ های کاهش استاندارد از طریق معادله زیر بدست می آید.

E_red = E^۰_red – (RT / zF) ln (γ_Red  C_Red / γ_Ox C_Ox)

= E^۰_red – (RT / zF) (ln γ_Re / γ_Ox + ln C_Red / C_Ox)

E_red = (E^۰_red – (RT / zF) ln γ_Re / γ_Ox) – RT / zF ln C_Red / C_Ox)

جالب است بدانید که در رابطه فوق می توان به جای عبارت ریاضی E^۰_red – (RT / zF) ln γ_Re / γ_Ox)، عبارت E^۰‘_red را قرار داد که به آن پتانسیل‌ کاهش استاندارد رسمی گفته می شود.

E_red = E^۰′_red – RT / zF ln C_Red / C_Ox)

 

معادله نرنست و ثابت تعادل

انرژی آزاد گیبس (ΔG) به کمک رابطه زیر به اختلاف پتانسیل مربوط می شود:

ΔG = −nFE

که در آن، E بیانگر اختلاف پتانسیل سلول، n بیانگر تعداد الکترون ‌های انتقالی در واکنش و F بیانگر ثابت فارادی (۹۶۴۸۵.۳۳۲۱۲۳۳۱۰۰۱۸۴ C mol^−۱) است. در شرایط استاندارد، رابطه فوق به صورت زیر می شود:

ΔG^۰ = −nFE^۰

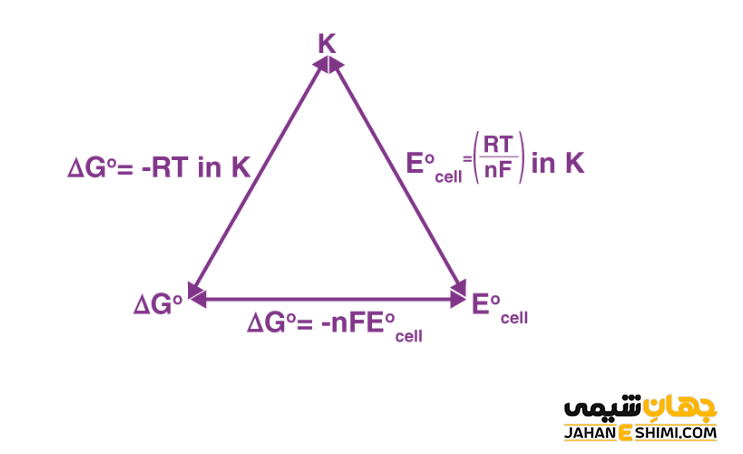
از طرفی دیگر، انرژی آزاد استاندارد گیبس به صورت زیر به ثابت تعادل (K) مربوط می شود:

ΔG^۰ = -RT ln K_eq

با جایگذاری ΔG^۰ = −nFE^۰ در معادله بالا داریم:

nFE^۰ = -RT ln K_eq−

ln K_eq = nFE^۰ / RT

در نهایت با تبدیل ln به Log در دمای اتاق، رابطه زیر بدست می آید:

Log _۱۰ ^Keq = n E^۰ / ۰.۰۵۹۲ V

رابطه بالا نشان می دهد که ثابت تعادل یک واکنش شیمیایی با پتانسیل استاندارد متناسب است. در اینصورت دو حالت ممکنست پیش آید.

• حالت اول؛ ثابت تعادل بزرگتر از یک (K > 1) و پتانسیل استاندارد واکنش مثبت(E^۰ > 0)  باشد. در این صورت، واکنش شیمیایی مورد نظر به سمت محصولات پیش ‌روی می‌ کند.
• در حالت دوم؛ ثابت تعادل واکنش کوچکتر از یک (K < 1) و پتانسیل استاندارد واکنش نیز منفی (E^۰ < 0)  باشد. در این صورت، واکنش شیمیایی مورد نظر به سمت واکنش ‌دهنده‌ ها پیش ‌روی می‌ کند.

 

جالب است بدانید که دو نتیجه بالا با اصل لوشاتلیه مطابق است. به بیان ساده تر، زمانیکه در یک سیستم تعادلی تغییری بوجود آید، این سیستم به منظور کاهش اثر این تغییر، تعادل را در جهت مخالف حرکت می دهد.

 

محدودیت‌ های رابطه نرنست

در محلول های رقیق، رابطه نرنست را می توان به صورت مستقیم بر حسب غلظت بیان کرد (زیرا ضرایب فعالیت نزدیک به واحد هستند). اما توجه داشته باشید که در غلظت های بالاتر، بایستی از فعالیت های واقعی یون ها بهره برد. این موضوع، استفاده و کاربرد از رابطه نرنست را پیچیده می ‌کند. زیرا همانطور که می دانید، تخمین و تعیین فعالیت ‌های غیر ایده ‌آل یون‌ ها اغلب به اندازه‌ گیری ‌های تجربی نیاز دارد. همچنین معادله نرنست تنها زمانی می تواند مورد استفاده قرار گیرد که جریان خالصی از الکترود وجود نداشته باشد. زیرا فعالیت یون‌ ها در سطح الکترود، زمانیکه جریان وجود دارد تغییر می ‌کند. بدین شکل، شرایط پتانسیل اضافی بیش از حد و تلفات مقاومتی نیز وجود خواهند داشت که در پتانسیل اندازه گیری شده مشارکت دارند.

علاوه بر آن، در غلظت های بسیار پایین یون های تعیین کننده پتانسیل، پتانسیل پیش بینی شده توسط رابطه نرنست به سمت بینهایت نزدیک می شود. این حالت از لحاظ فیزیکی بی معنی می باشد. زیرا در چنین شرایطی، چگالی جریان مبادله بسیار کم خواهد بود و ممکن است تعادل ترمودینامیکی لازم جهت برقراری رابطه نرنست وجود نداشته باشد. الکترود را در چنین مواردی غیر قابل تنظیم می نامند.

 

مثال معادله نرنست

یک الکترود روی در یک محلول اسیدی ۰/۸ مولار Zn^+۲، به کمک یک پل نمکی به یک الکترود نقره ای در محلول ۱/۳۰ مولار ⁺Ag، متصل شده است. ولتاژ اولیه سلول گالوانی را در ۲۹۸ کلوین بدست آورید.

Zn^+۲ (aq) + 2e^– → Zn (s)    E = – 0.76 V

Ag ⁺ (aq) + e^– → Ag (s)      E = + 0.80 V

دقت داشته باشید که برای اینکه سلول مورد نظر به عنوان گالوانیزه باشد، بنابراین E^۰ باید مثبت شود. این امر در صورتی امکان پذیر است که عنصر روی اکسید و عنصر نقره احیا گردد. بنابراین نیم واکنش های اکسایش و کاهش به شکل زیر تصحیح می شوند.

Zn (s) → Zn^+۲ (aq) + 2e^–    E_ox = + ۰.۷۶ V

Ag ⁺ (aq) + e^– → Ag (s)      E_Red = + ۰.۸۰ V

واکنش کل سلولی عبارت است از:

Zn (s) + 2Ag⁺ (aq) → Zn^+۲ (aq) + 2Ag (s)

E^۰ نیز از ترکیب دو پتانسیل استاندارد بدست می آید (E_ox  + E_Red = ۱.۵۶ V). مقدار عددی خارج قسمت واکنش هم برابر است با:

Q = (0.80) / (1.30)^۲ → Q = (0.80) / (1.69) → Q = 0.47

اکنون، با استفاده از معادله نرنست  داریم:

E_cell = E^۰_cell – (۰.۰۵۹۲V / n) Log _۱۰^Q

E_cell = ۱.۵۶ V – (0.0592 / 2) log (0.47) → E = 1.57 V

 

کاربرد های معادله نرنست

همانطور که بیان شد، این معادله جهت محاسبه ولتاژ و یا غلظت یکی از اجزای سلول الکتروشیمیایی، کاربرد دارد. همچنین، زمانیکه جهت محاسبه پتانسیل یک یون با بار z در سراسر غشاء استفاده شود، کاربرد فیزیولوژیکی پیدا می کند. این پتانسیل با استفاده از غلظت یون در داخل و خارج سلول تعیین می شود. معادله آن به شکل زیر است.

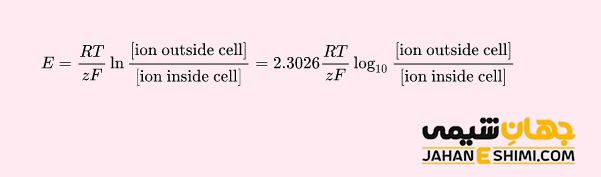
رابطه نرنست همچنین در بحث علمی در مورد همجوشی سرد نیز نقش دارد. علاوه بر آن، این معادله امکان محاسبه میزان واکنش بین دو سیستم ردوکس را نیز فراهم می‌ کند. در واقع، می‌ تواند به عنوان مثال برای ارزیابی اینکه آیا یک واکنش خاص به پایان می ‌رسد یا خیر مورد استفاده قرار گیرد. همانگونه که می دانید، در تعادلات شیمیایی، نیرو های الکتروموتور (emf) دو نیم سلول برابر است. از این جهت می توان ثابت تعادل یک واکنش شیمیایی و در نتیجه میزان واکنش را نیز محاسبه نمود.